5 简易方程

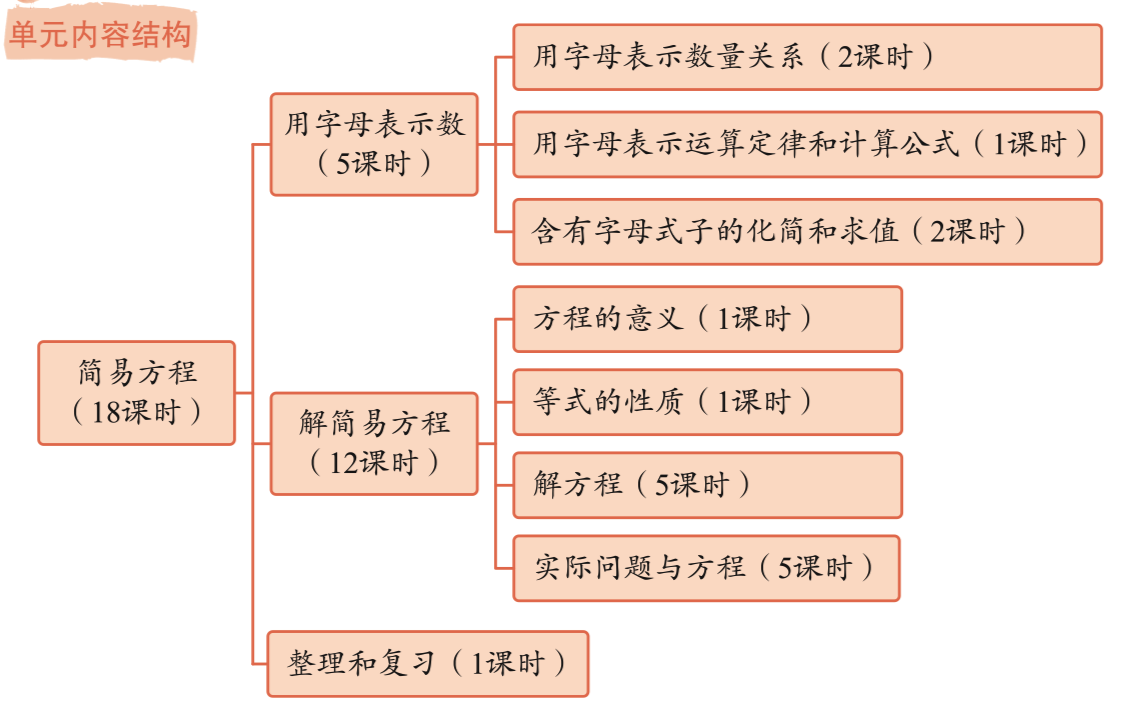
单元内容结构

电子教材

单元作业目标

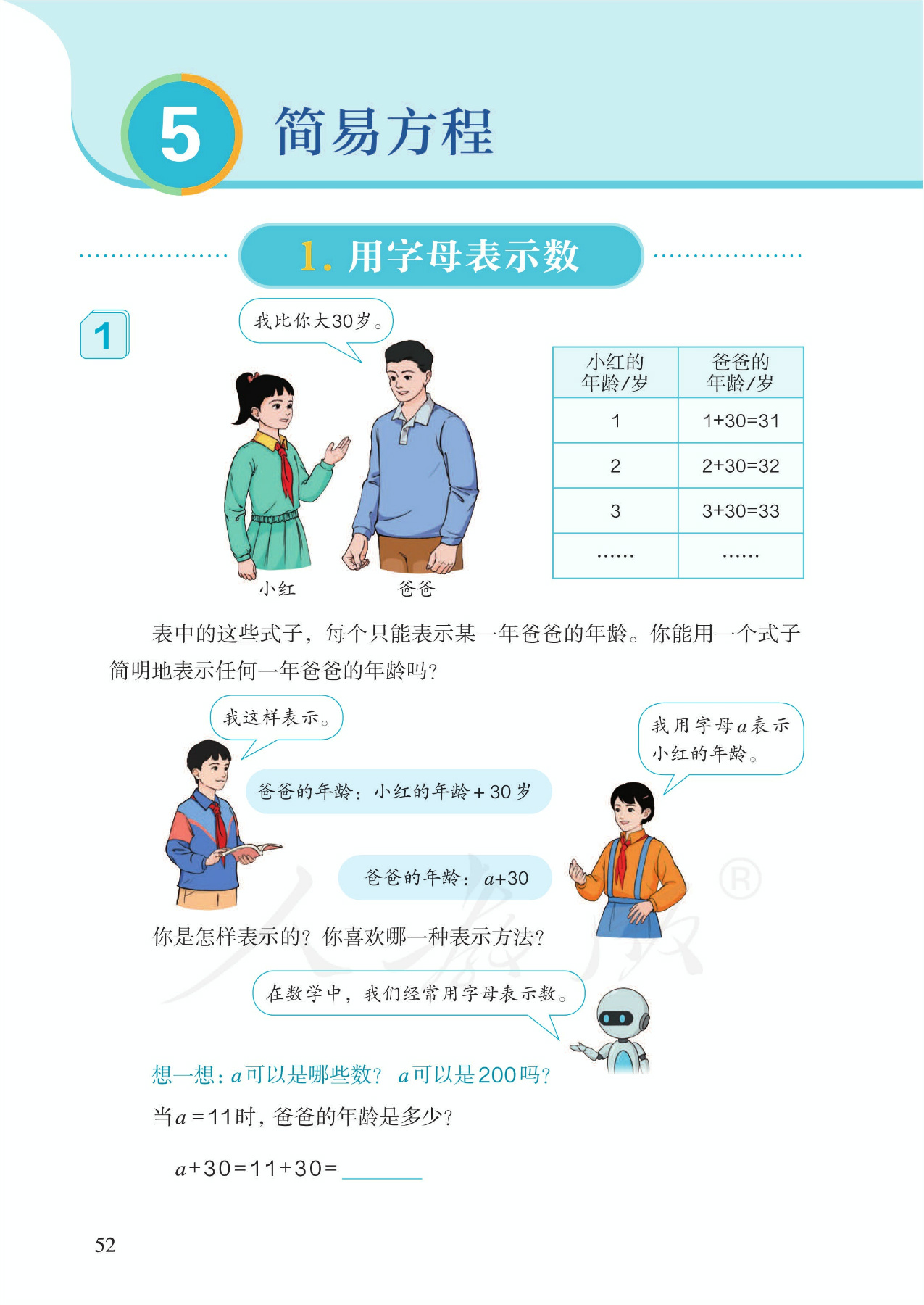
1.能结合具体情境，用含有字母的式子表示常见的数量关系

2.能用含有字母的式子表示学过的运算定律和计算公式

3.能对含有字母的式子进行化简并求值

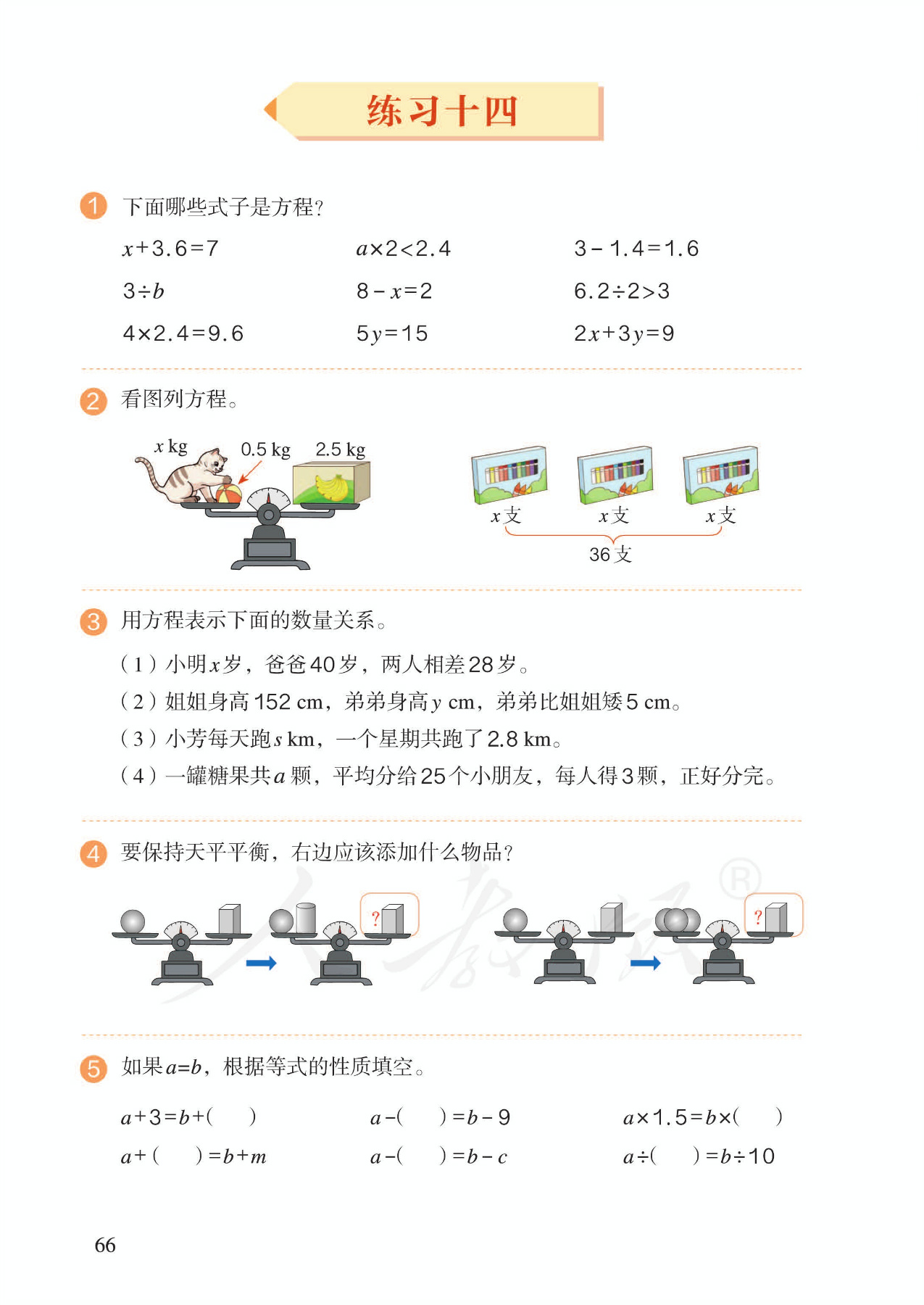
4.能正确判别“方程”与“等式”，理解“方程的解”和“解方程”的不同含义

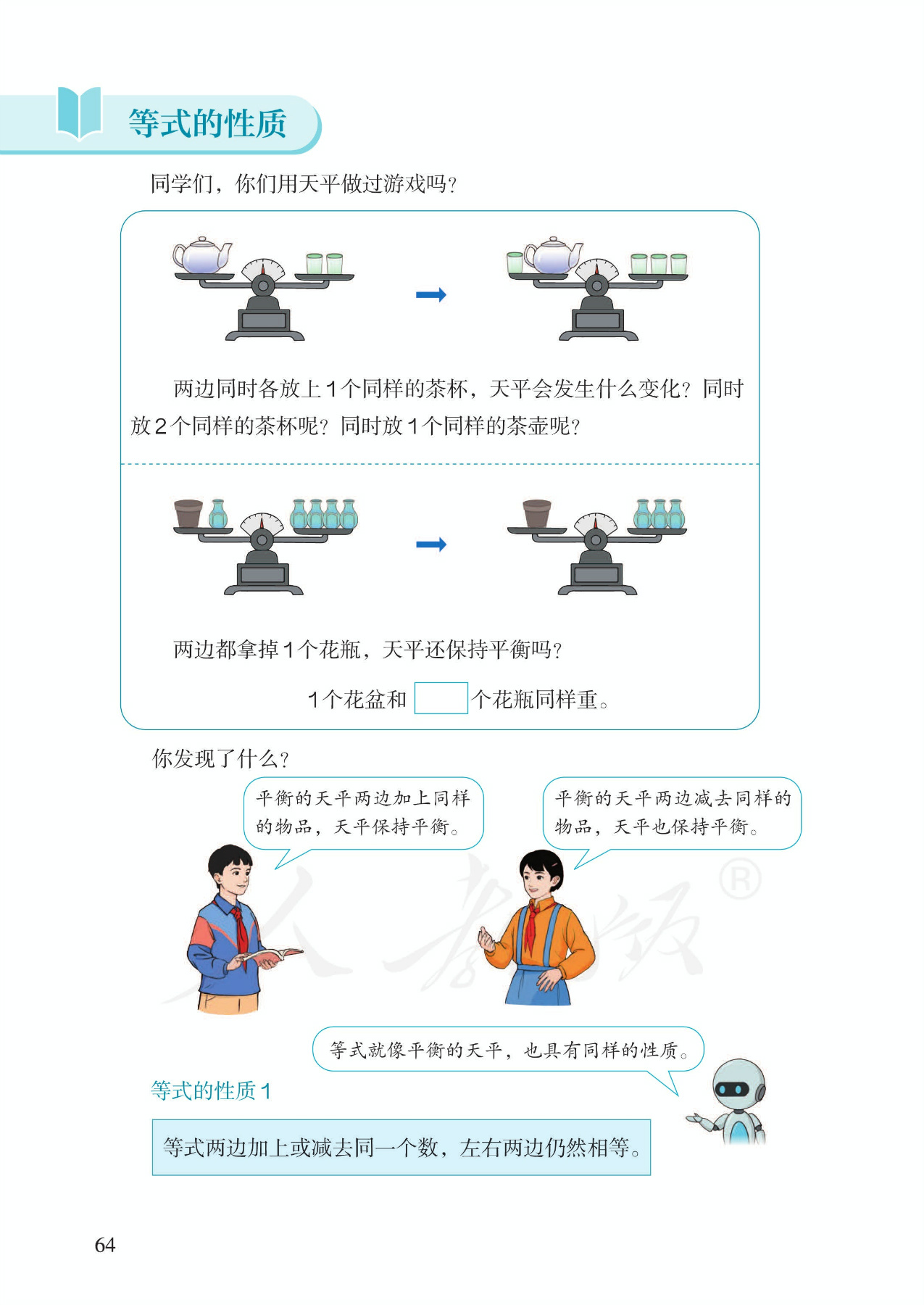
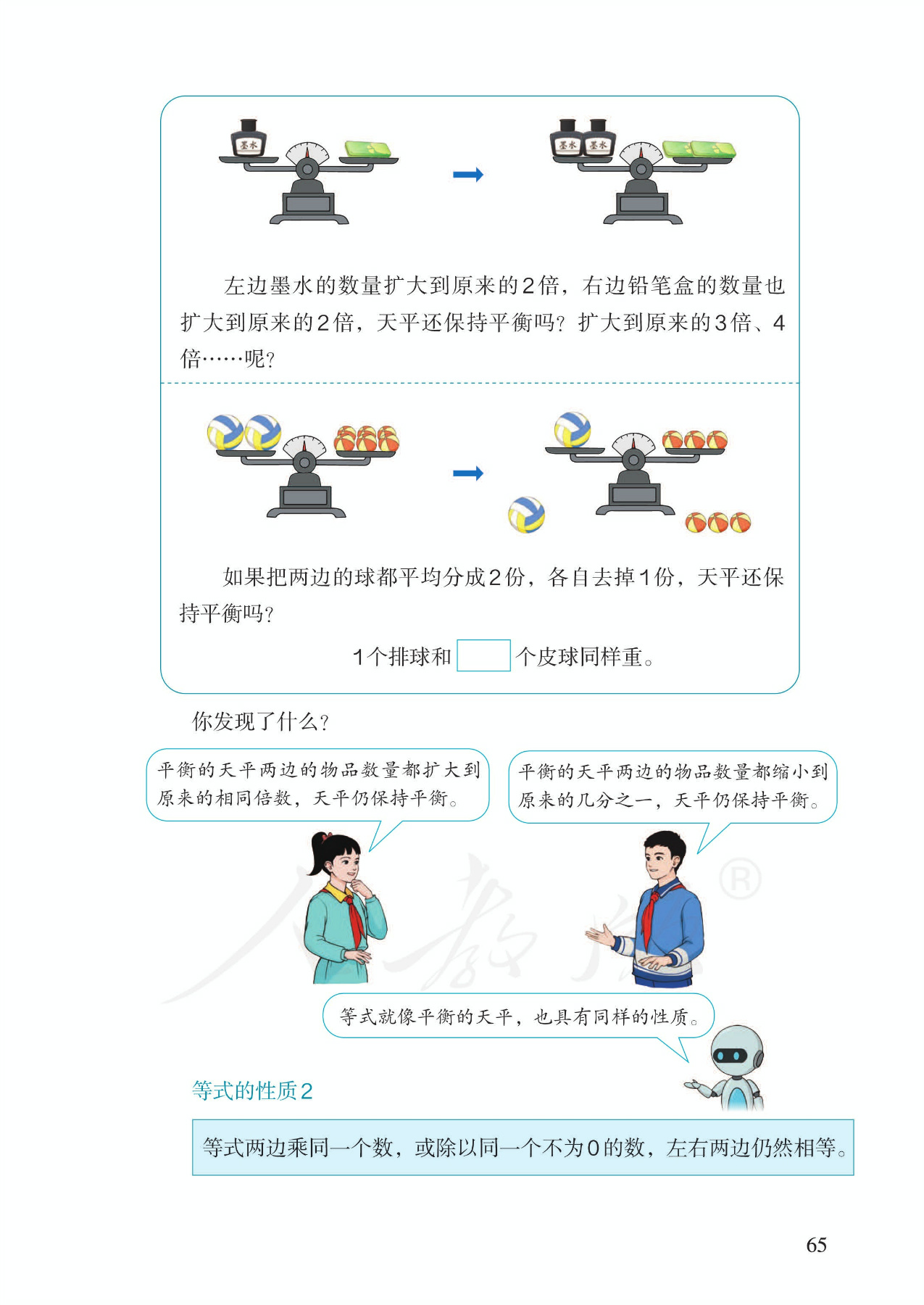
5.能理解等式性质，并应用等式性质进行等式变形

6.能正确运用等式的性质以规范的格式解一步方程，并正确检验

7.能正确运用等式性质有序解答两步或三步方程，并正确检验

8.能根据问题情境建立等量关系，并列方程解决简单的实际问题

教材解读

本单元是在学生具备了一定的算术知识（如整数、小数的四则运算及其应用），已初步接触了一点代数知识（如用字母表示运算律，用“○”“△”或“□”表示数）的基础上，教学用字母表示数和解简易方程。内容上分为两部分，第一部分的主要内容是用字母表示数和数量关系、表示运算律和计算公式；第二部分的主要内容是方程的意义、等式的性质和解简易方程，以及列方程解决一些比较简单的实际问题。

教科书在内容编排上充分尊重学生的认知规律，先学习用字母表示一个特定的数，逐步过渡到学习用字母表示一般数、运算律和计算公式，等学生有了一定的基础，再学习用含字母的式子表示数量和数量关系。这样由易到难，逐层深入，便于学生有效掌握所学知识。

用字母表示数，是由具体的数和运算符号组成的式子过渡到含有字母的式子，使学生建立初步的符号感，是学生学习数学的一个转折点，也是认识上的一次飞跃。学习方程既是学生进一步接触代数思想，对所学四则运算意义和数量关系的进一步深化，又是为今后学习代数知识打基础，在知识衔接上具有重要作用。

学情分析

学生已经学习了一定的算术知识，初步接触了一些代数知识，在日常生活中也接触到了用字母表示数，如扑克牌中的A，J，Q，K分别表示1，11，12，13。这些都是学习本单元的基础。

用字母表示数对于小学生来说，是学习代数初步知识的起步。让学生从具体的、确定的数过渡到用字母表示抽象的、可变的数，对学生来说是认识上的一个飞跃，而因为认知过程比较抽象，学生理解起来会有一定的难度。特别是用含有字母的式子来表示数量关系，更让学生感到困难。因此，教师要充分利用学生原有的相关认识基础来教学。

教学策略

1.有意识地渗透数学的思想方法。在本单元的教学中，从一开始就应有意识地利用教学内容的特点，渗透数学抽象思想，启发学生在抽象概括数量关系的过程中理解结论的一般性，体会字母、符号的使用是数学表达和进行数学思考的重要形式。教学时，应要求学生做得对、说得清，从而在理解变形依据、过程的基础上掌握所学方程的解法。

2.注意掌握教学目标的适用性。从代数角度考查本单元的教学内容，不难发现内容本身有很大的拓展空间。因此，教师在确定各课时的教学目标时，应参照教科书和本单元的教学目标，同时还应从本班学生的实际情况出发，把教学目标定在学生的最近发展区内。例如，在教学用方程解决问题时，教师可以补充一些联系实际的问题，特别是补充一些具有地方特色的实际问题。但这些问题的数量关系不能过于复杂，必须是学生能够理解的；由这些问题所得到的方程，形式一般不宜难于教科书，以免加重学生的学习负担。

3.本单元的解简易方程部分的教学，增加了求减数和求除数的知识，是这一单元的一个难点，学生很难理解，教师在讲解这类题时先利用等式的性质，讲到x在右边时，左右两边调换顺序可使x在左边，再次利用等式的性质求出方程的解，在上课时一定要让学生理解为什么得到这一步，还要多练多讲，学生才能真正理解。

单元目标

1.使学生初步认识用字母表示数的作用，发展符号意识，能够用字母表示学过的运算定律和计算公式，能够在具体的情境中用字母表示常见的数量关系。初步学会根据字母所取的值，求含有字母式子的值。

2.使学生初步了解方程的作用，初步理解等式的基本性质，能用等式的基本性质解简易方程。在这一过程中初步体会化归思想。

3.使学生感受数学与现实生活的联系，初步学会列方程解决一些简单的实际问题。在这一过程中获得数学建模的初步体验。培养学生根据具体情况，灵活选择算法的意识和能力。

例题分析

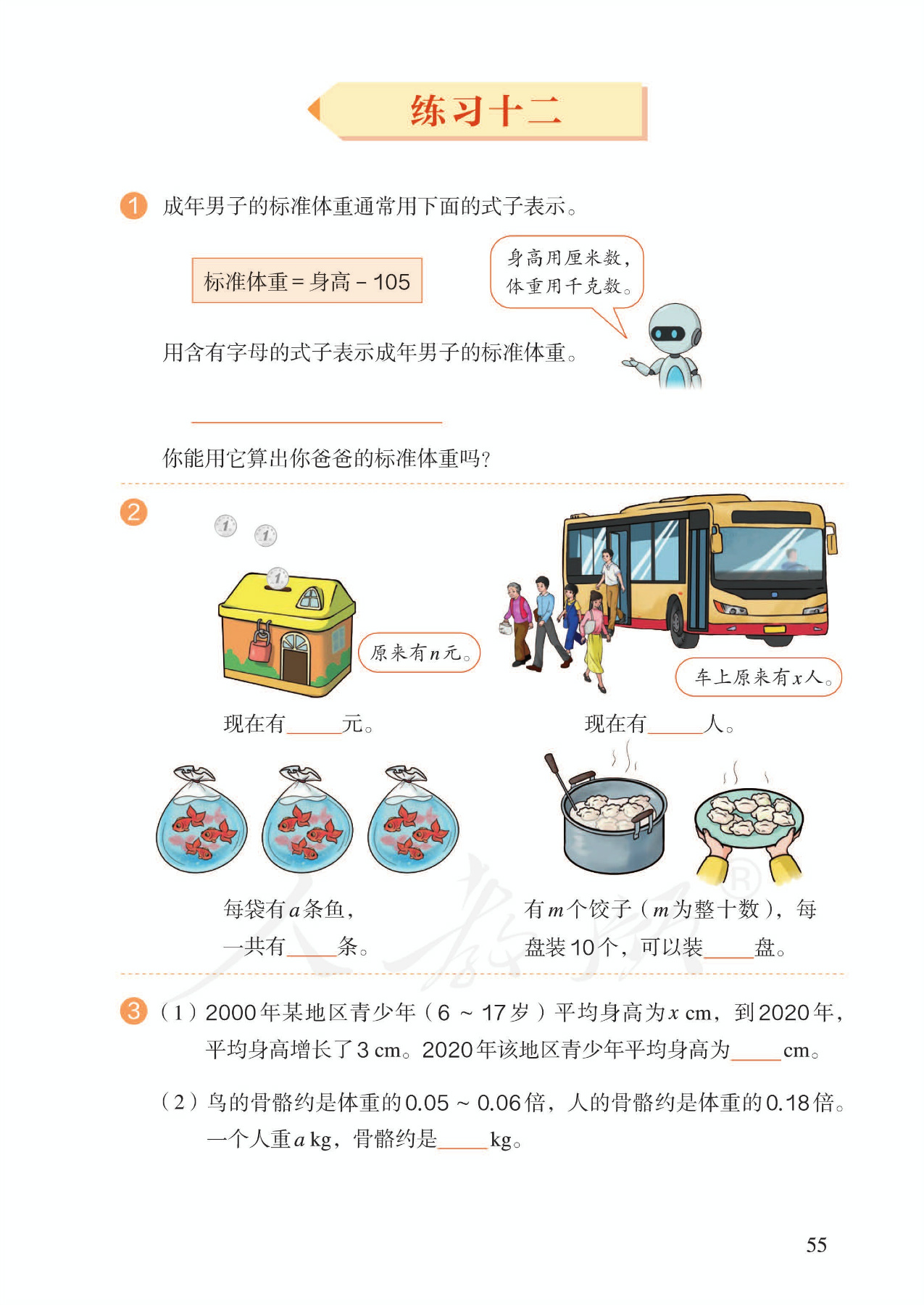
1.用字母表示加减的关系。具体编排体现“具体、一般、具体“的过程。(1)重视抽象概括。用含有字母的式子表示数量关系和一个量，这是列方程的基础。(2)渗透函数思想。让学生体会：a+30随着a的变化而变化，它们之间一一对应，以渗透函数思想。(3)取值范围。关于字母的取值范围应该让学生明确，在一个实际问题中，字母的取值范围是由实际情况决定的。(4)代入求值。帮助学生进一步理解，含有字母的式子也可以表示一个具体的数量。

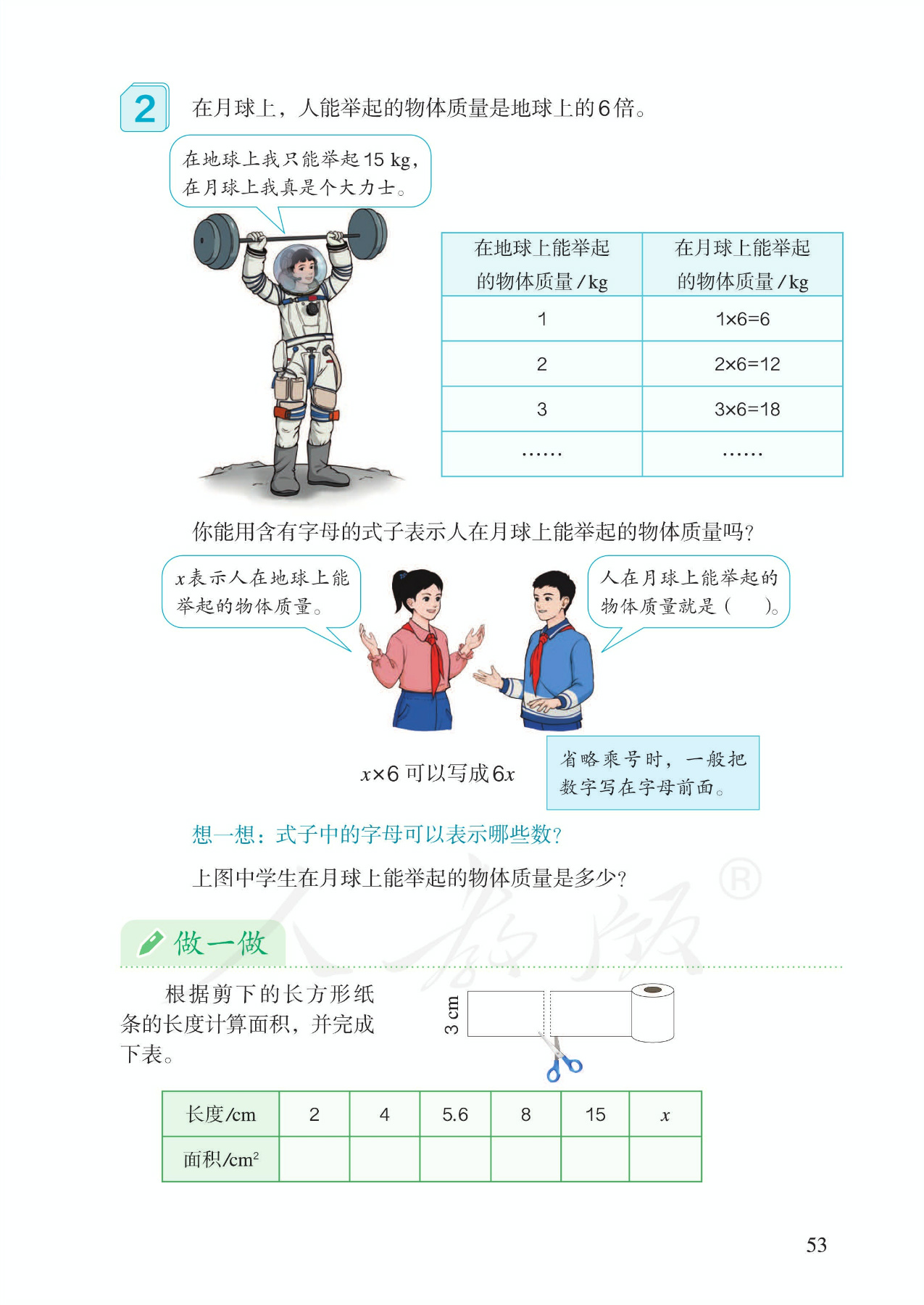
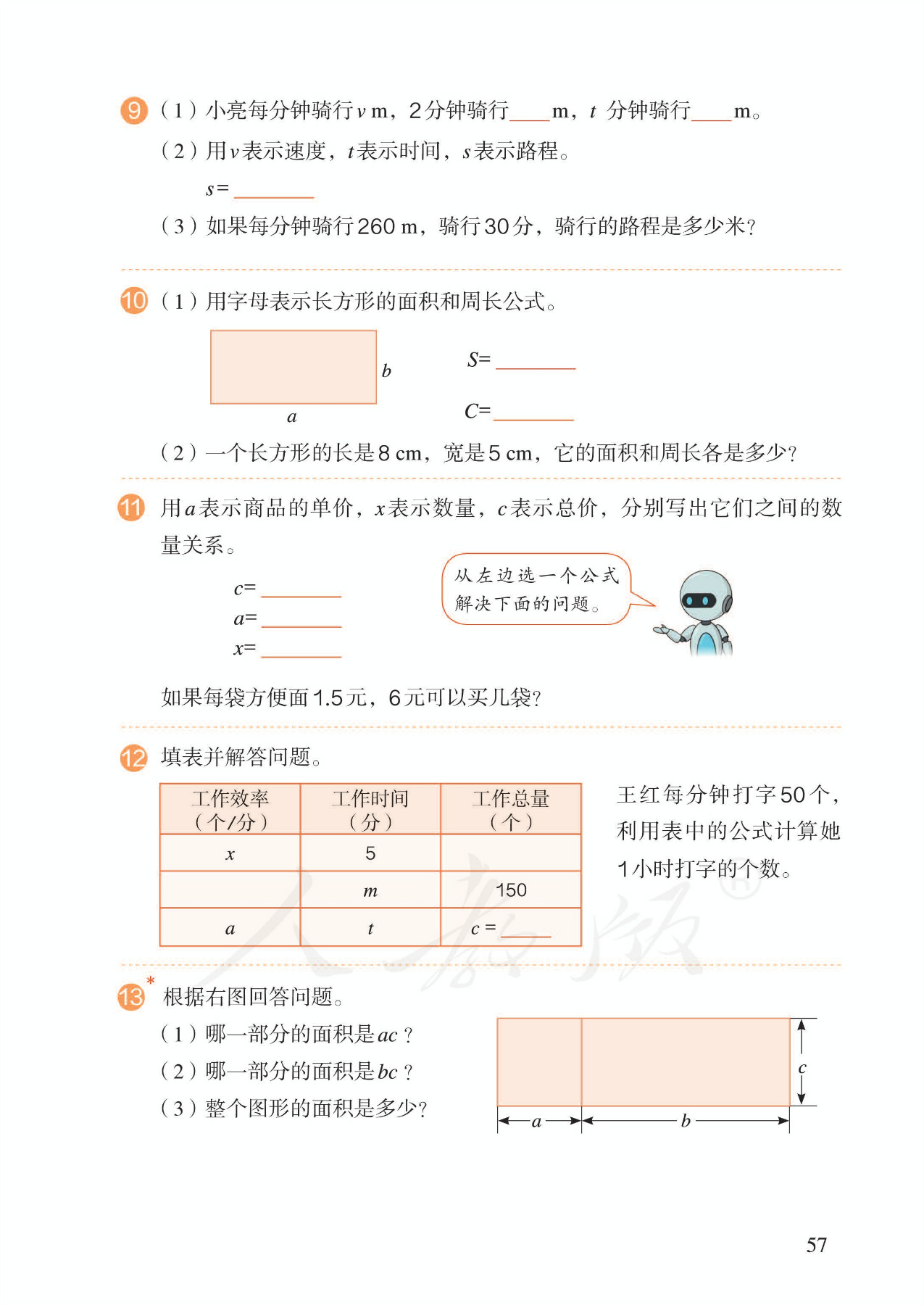
2.乘除的数量关系。(1)编排和例1相同。同样是从具体到一般的抽象、归纳过程，再从一般到具体的代入求值。(2)介绍字母与数相乘的习惯写法。

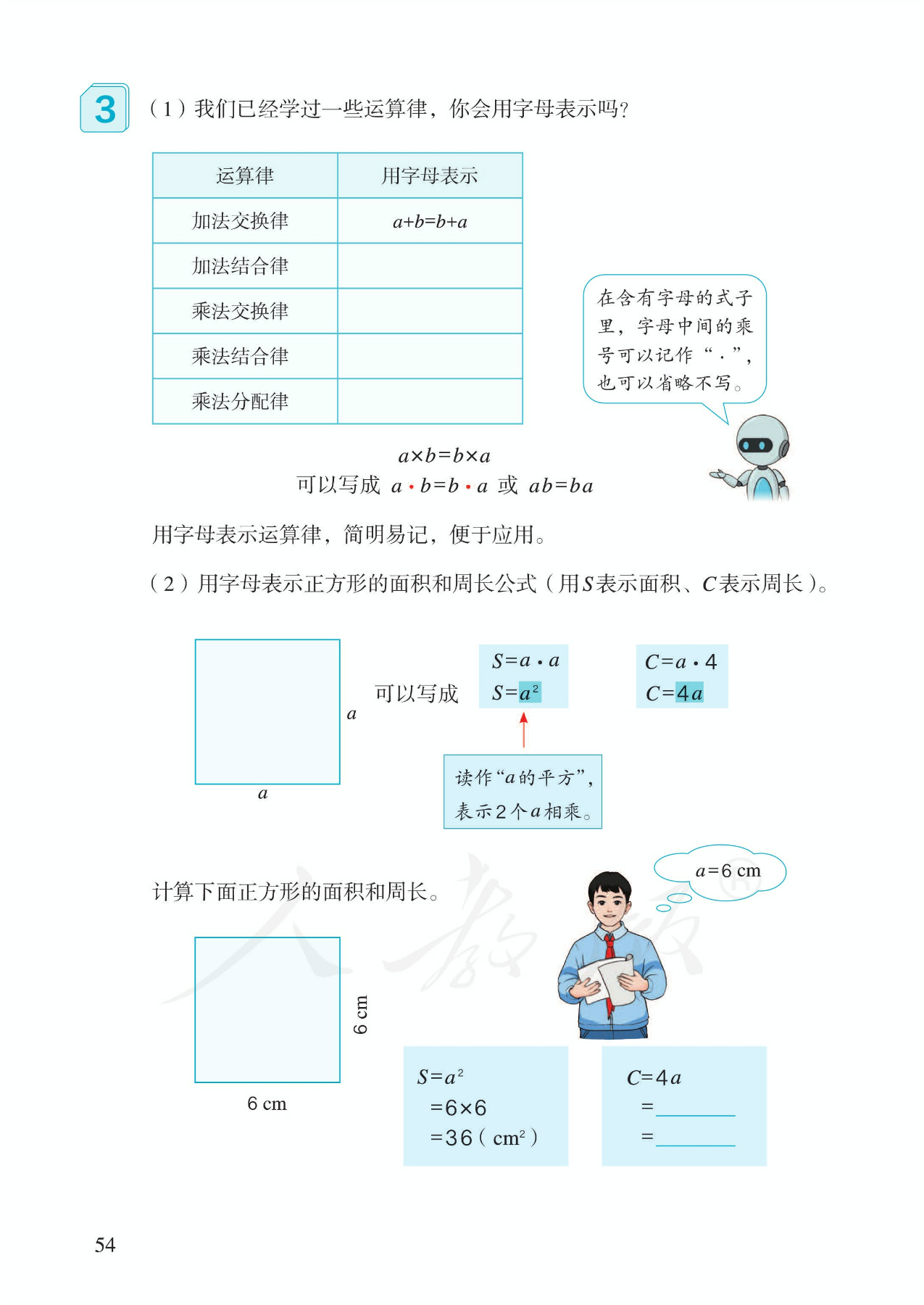
3.运算定律、计算公式。(1)体会数学符号语言的优越性。(2)代入求值。并介绍平方的书写方法，数与字母相乘的书写习惯。

4.两级运算。让学生学会用含有字母的式子表示稍复杂的数量关系，为后面列方程解决实际问题作准备。

5.两积之和。引导学生化简式子。

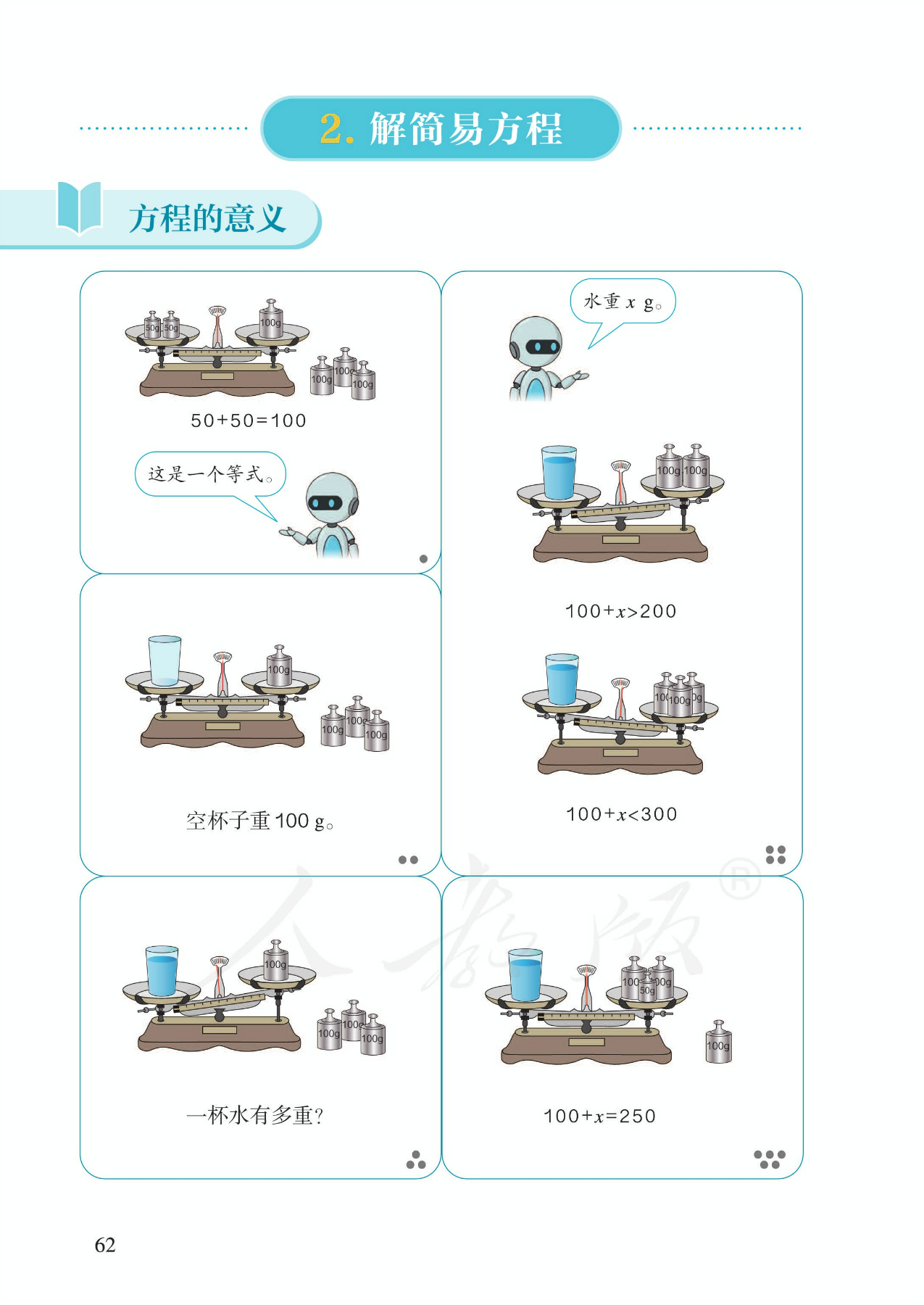
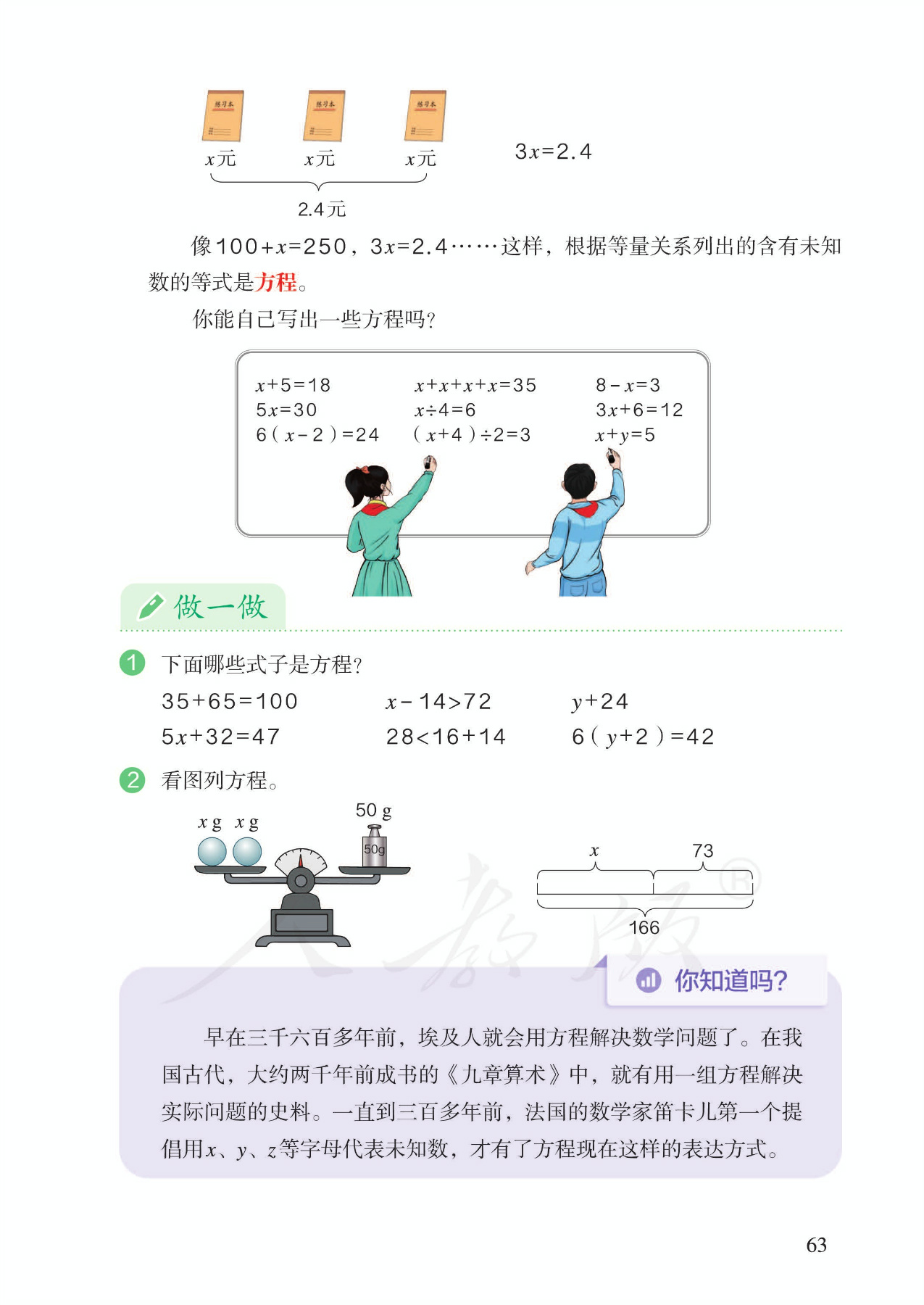
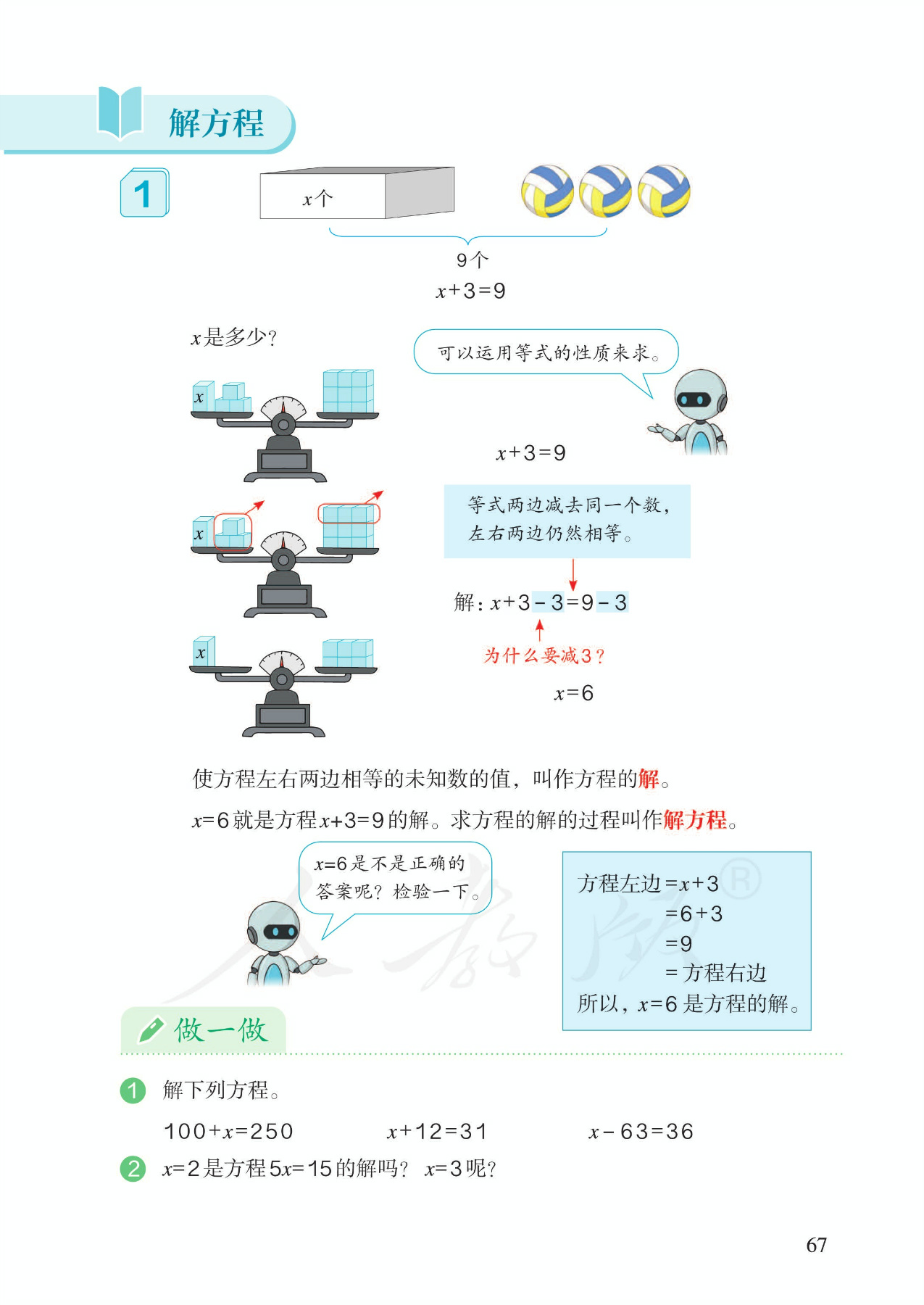
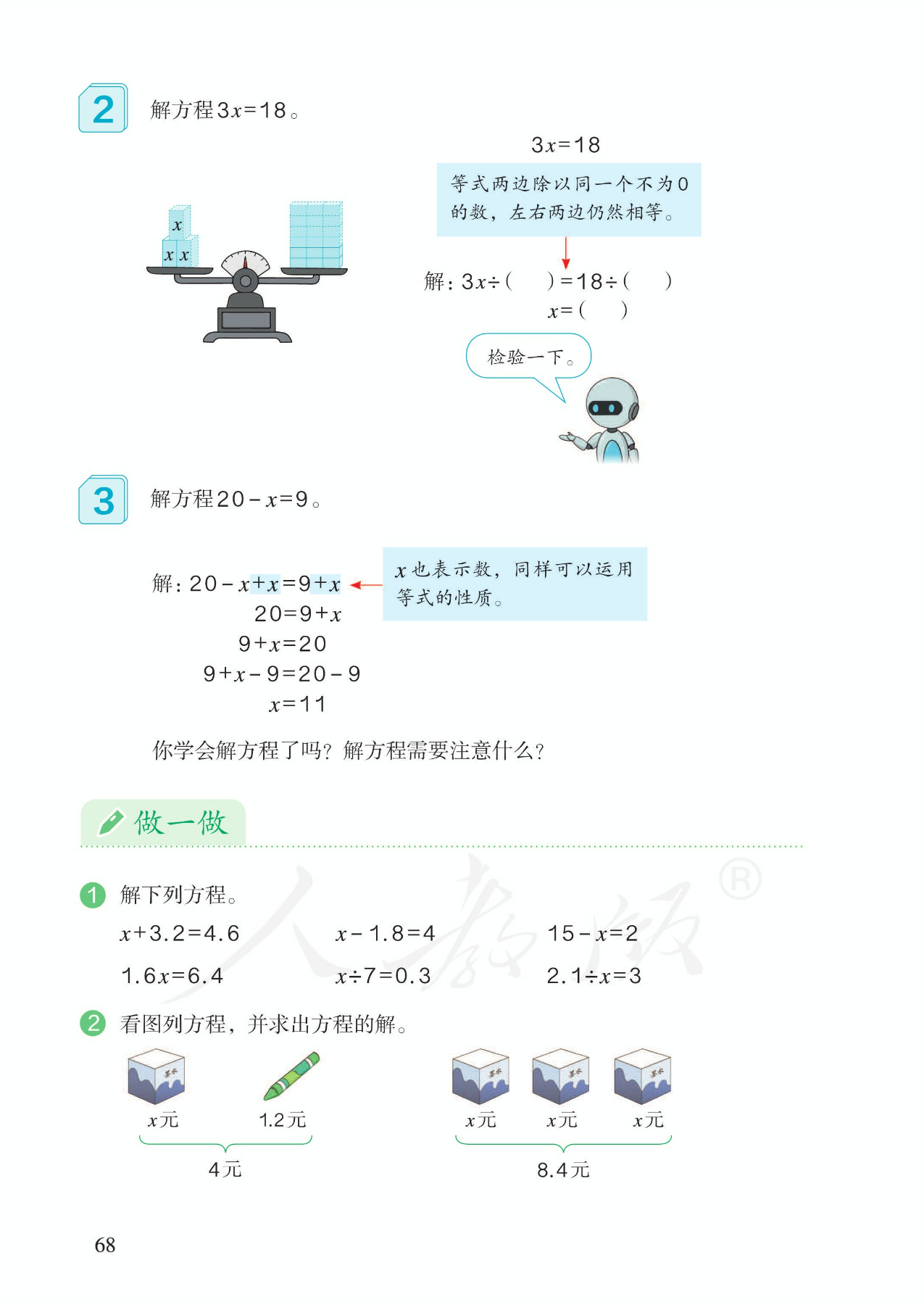
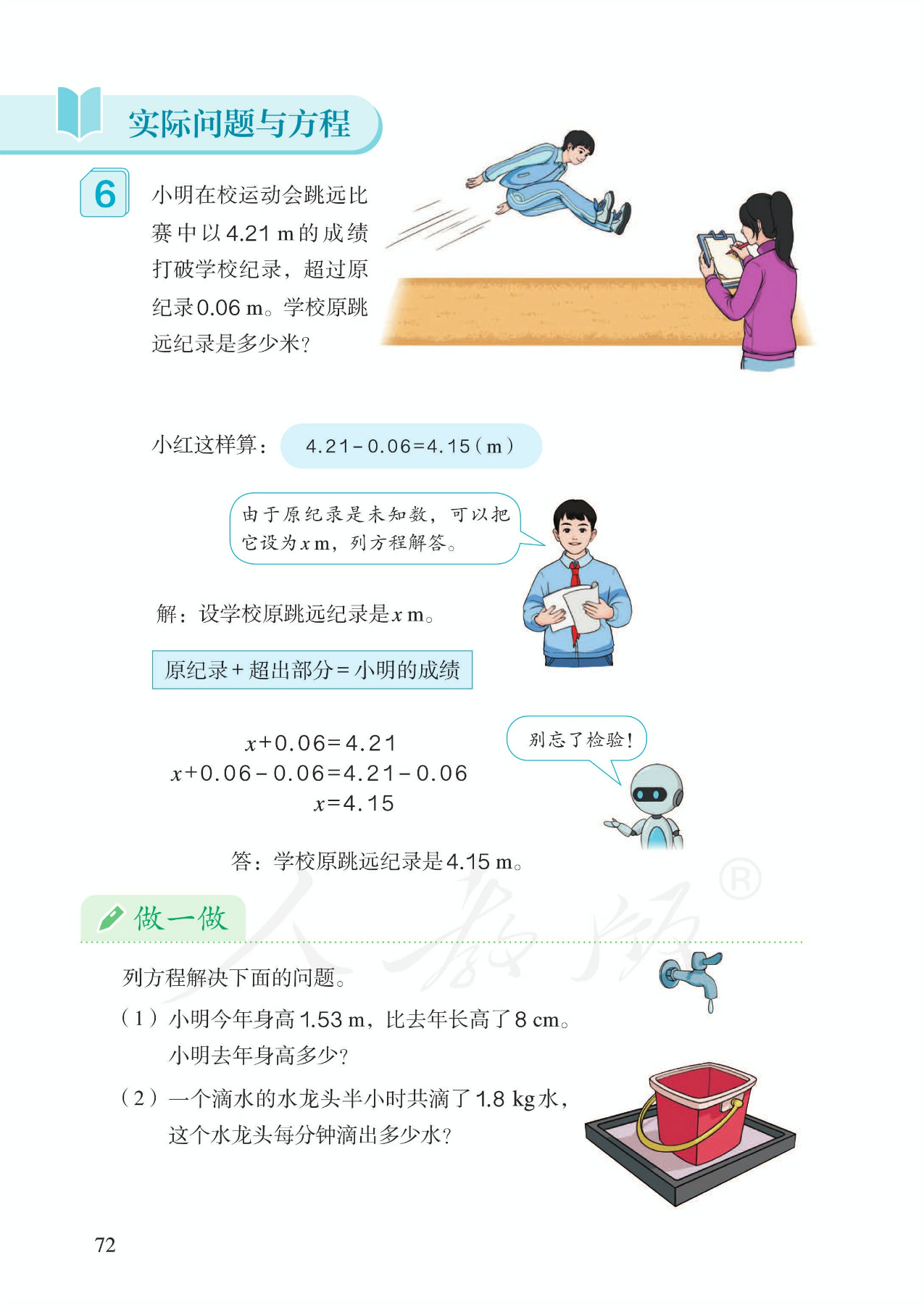
6.解方程，例1：解形如x+a=b的方程。借助三幅天平演示图展现了解方程的完整思考过程。明确指出要根据等式性质来解方程。暂时避开算法多样化的讨论。

7.解方程，例2：解形如ax=b的方程。

8.解方程，例3：解形如a-x=b的方程。重点突出转化思想。及时总结解方程的思考方法(利用等式性质)、解题步骤、要注意的问题。

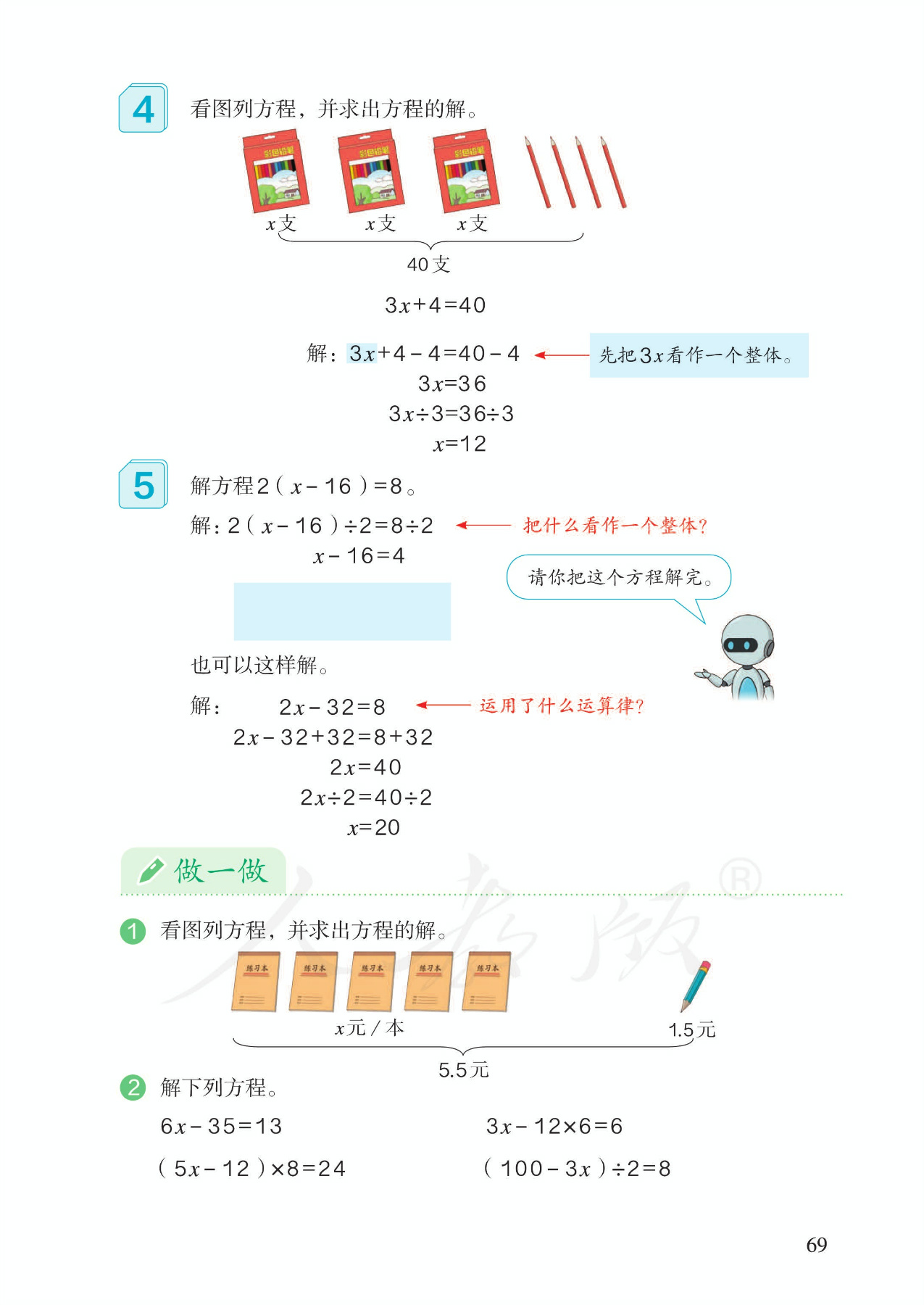
9.解方程，例4：解形如ax+b=c的方程。

10.解方程，例5：解形如a(x-b)=c的方程。教学重点是把什么看作一个整体。

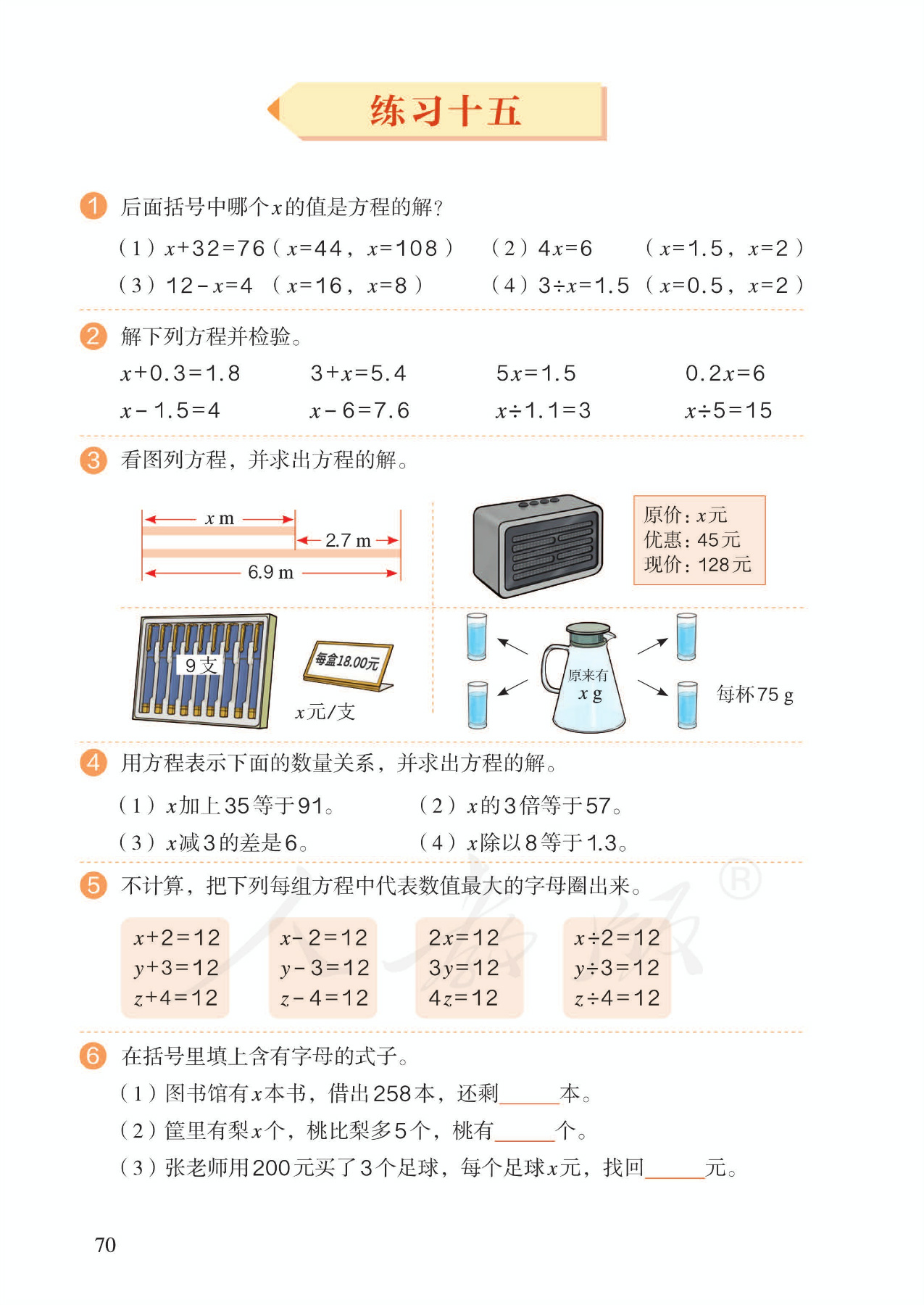
11.实际问题，例1：基本类型。①经历列方程解决实际问题的基本方法。②体会列方程解决问题的特点：用字母表示未知数，未知数参与列式。其中寻找等量关系是列方程的关键。③淡化算术方法和列方程方法的对比。

12.实际问题，例2：列方程解形如ax±b=c的问题。①体会优越性。②注重数量关系的分析。有必要的话，可以画线段图帮助分析。③总结列方程解决实际问题的基本步骤。

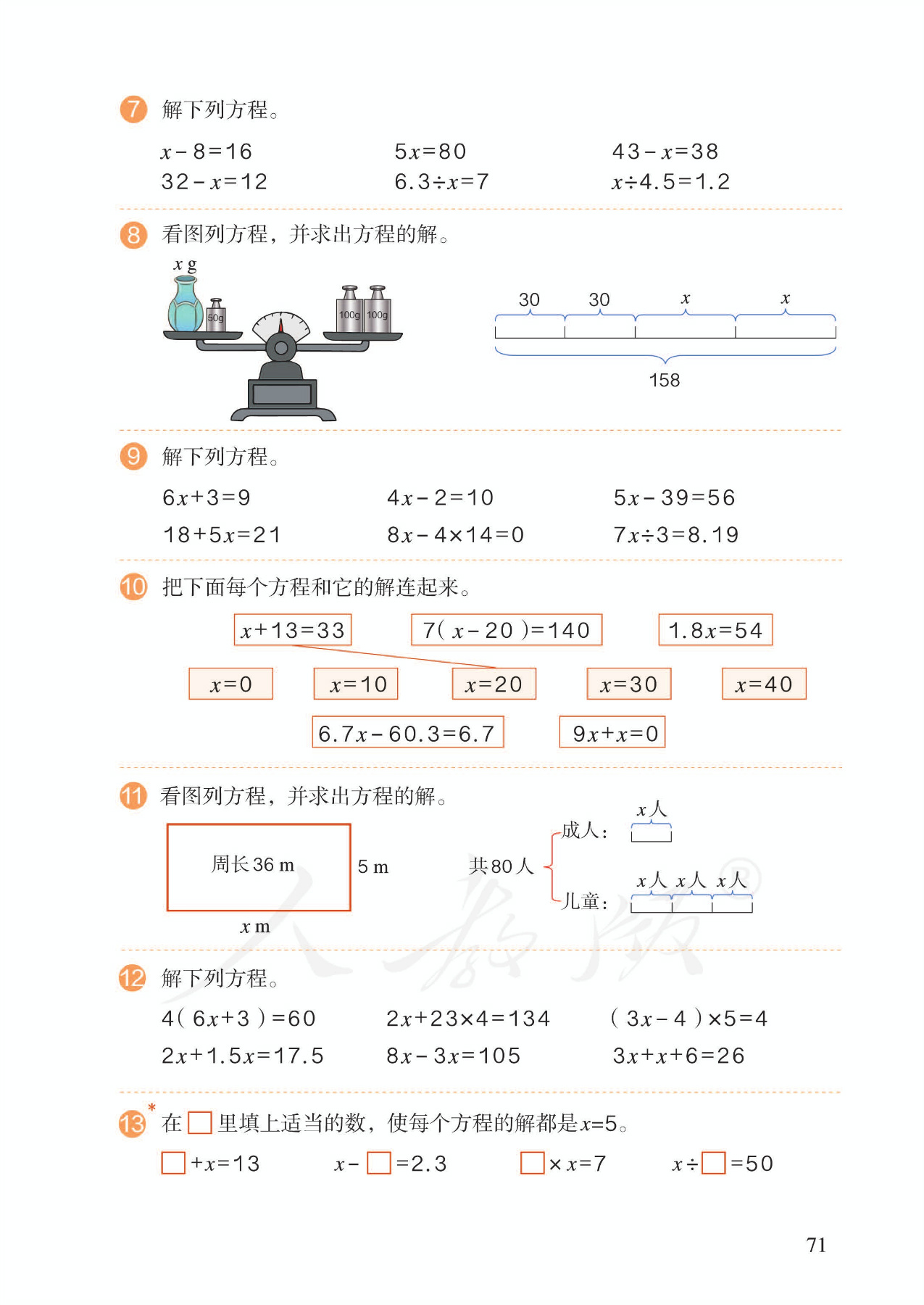
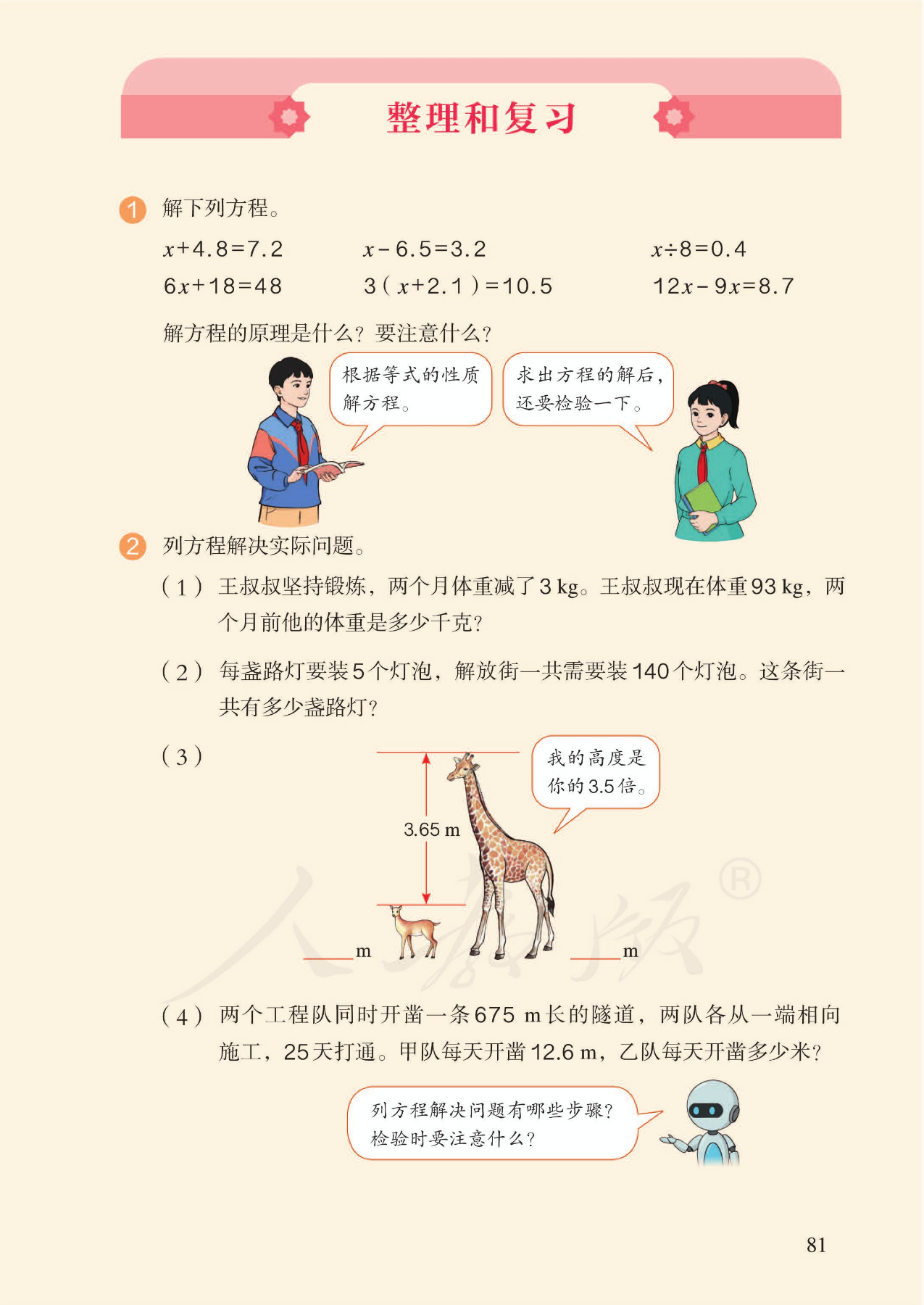
13.实际问题，例3：列方程解形如ax+ab=c的问题。理解了两积之和的数量关系，也就容易理解两积之差、两商之和(差)的数量关系。可以根据分配律，得到含小括号的方程。具有举一反三的典型意义。

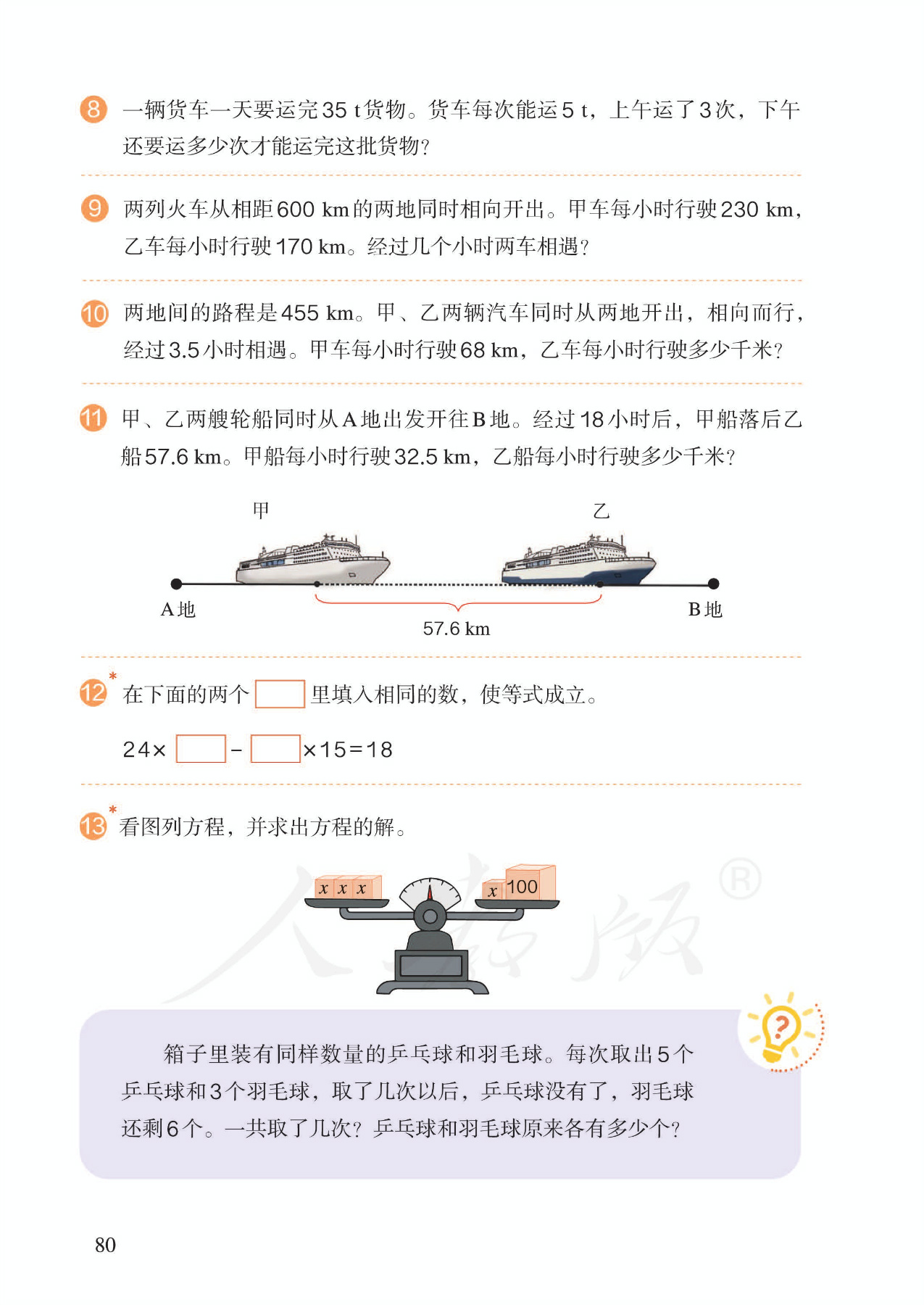
14.实际问题，例4：列方程解形如ax+bx=c的问题。①含有两个未知数。此类问题称为“和差、和倍、差倍问题”，其特点是：含有两个未知数，知道这两个未知数的倍数关系，以及它们的和或差，求两个未知数。②设未知数。解决这类问题，一般为了解方程方便，设倍数关系中的单位量为x。也可以利用线段图帮助学生思考。

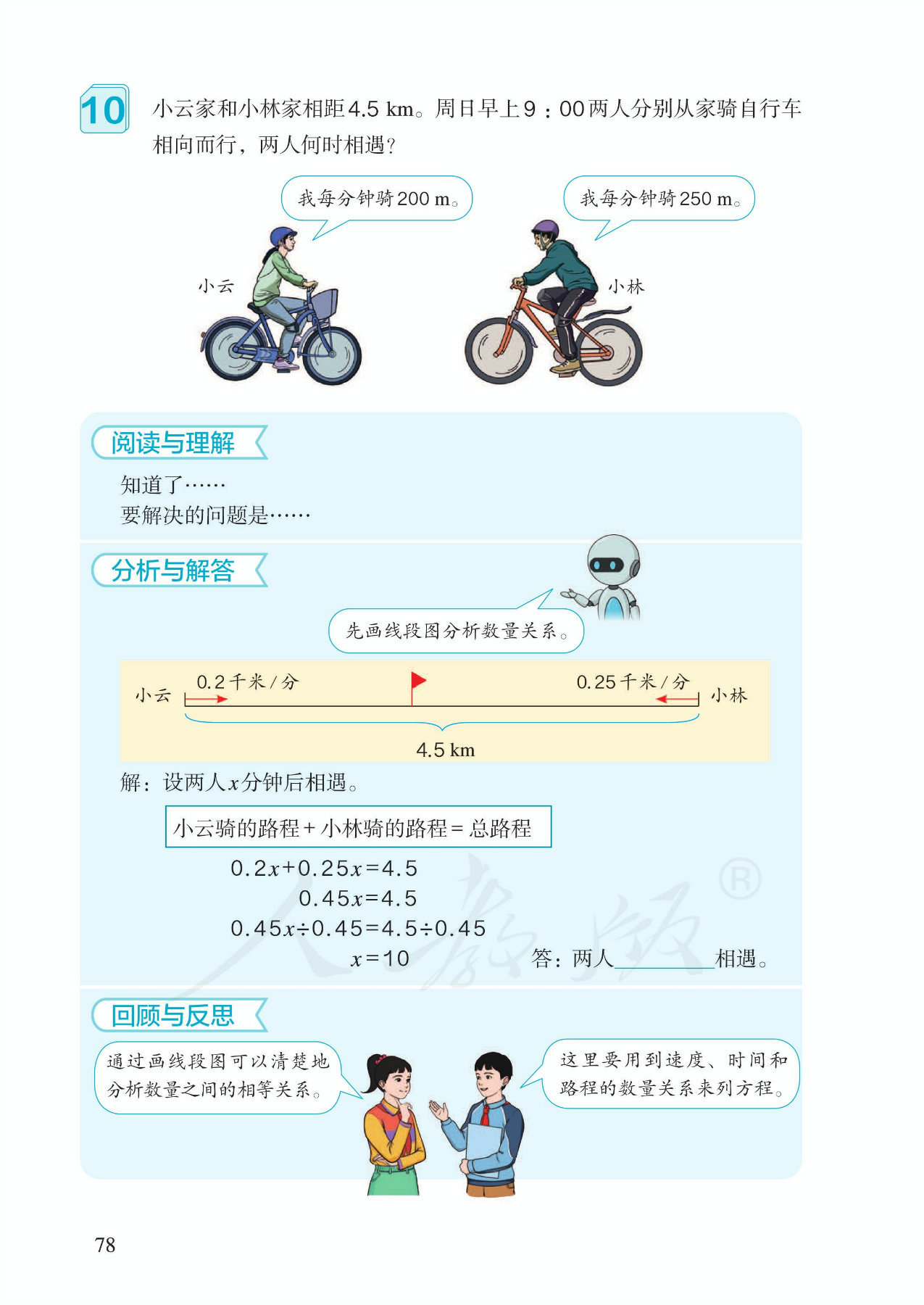
15.实际问题，例5：解决问题。行程中的相遇问题，重点是借助线段图来帮助学生分析数量关系，列出方程。

请 Ta 喝咖啡 ☕️

喝咖啡记录：